Scaling Quantum Optimization
Benchmarking VQE with MIMIQ
December 2024
Contribution from Anna Leonteva
Software Engineer at QPerfect
Many complex problems today—such as drug discovery and supply chain optimization—can be framed as optimization challenges, where the task is to identify the best solution among zillions of possibilities. However, traditional computing faces limits when the problem size becomes too large. Quantum computing has the potential to go beyond these limits by implementing Variational Quantum Algorithms [1], which use quantum principles to explore these vast solution spaces more efficiently. While the effectiveness of variational algorithms has been verified for small systems (10-20 qubits) [5], the biggest challenge they face is to prove their utility at relevant large scales (and in noisy quantum computers).
Since today’s quantum computers are either too small or too noisy, showing quantum advantage at scale requires quantum emulators capable of handling large systems. As we show in this blogpost for the particular example of the Variational Quantum Eigensolver (VQE) [2], QPerfect’s quantum emulator, MIMIQ, can simulate variational circuits of up to 100 qubits with high fidelity within minutes.
What is the Variational Quantum Eigensolver (VQE)?
Originally presented in [3], VQE is an optimization algorithm which combines quantum and classical computing to find the lowest energy state of a quantum system, a process known as energy minimization. For example, in quantum chemistry, this lowest energy state represents a molecule’s most stable configuration, which is crucial for predicting its reactivity and behavior. In finance, energy minimization translates into optimizing a portfolio to balance risk and return, while in logistics, it can mean finding the most efficient use of resources across a network.
How does VQE work?
Step 1: Quantum Circuit Execution – A quantum computer prepares a quantum state called an “ansatz” using gates with adjustable parameters. It then measures the energy of the system represented by a Hamiltonian. (Due to the probabilistic nature of quantum mechanics, multiple runs are required to accurately estimate the energy in a quantum computer, but one single run is enough in a quantum emulator.)
Step 2: Classical Optimization Loop – The measured energy is fed into a classical computer, which uses optimization algorithms (e.g., gradient descent) to adjust the quantum circuit parameters, aiming to reduce the system’s energy further.
This process is repeated, with the quantum and classical steps working together in a feedback loop. Each iteration aims to refine the quantum state, gradually lowering the energy until the algorithm (hopefully!) converges on the lowest possible energy—the optimal solution for the system.
Simulating Small vs. Large Circuits
To efficiently handle circuits of varying sizes, MIMIQ uses two simulation engines—State Vector and Matrix Product States (MPS).
Small Circuits: State Vector Engine
In this method, the entire quantum state is represented as a vector of complex numbers, where each number corresponds to a different basis state. This method is exact (up to numerical accuracy) because it stores and performs calculations on the full state of the system. For circuits with up to 20-30 qubits, the state vector approach is efficient. For circuits with 30+ qubits, simulating the full state vector becomes impractical due to the exponential growth of the state space, requiring vast memory and time resources.
Large Circuits: Matrix Product States (MPS) Engine
Matrix Product States (MPS) is a method that compresses the quantum state into a more efficient representation. Instead of tracking every possible state, MPS focuses on capturing the most important correlations between qubits.
Because of this, MPS excels in simulating large circuits with a high degree of structure—many circuits produce states where qubits have significant interrelationships and relatively low entanglement. MPS manages an exact representation when feasible, and for more complex states, it provides a controlled approximation with fidelity estimates—thus, we can balance scalability and precision without the exponential panic.
The most important parameter controlling the level of approximation of an MPS is the bond dimension. In essence, a larger bond dimension means the MPS can capture higher entangled states and reach higher accuracy, at the cost of memory requirements scaling quadratically with it.
Benchmarking VQE scalability with MIMIQ
Now that we’ve discussed how MIMIQ scales with two engines, let’s put this into action with a real benchmarking experiment on the MIMIQ cloud. We’ll start by examining the performance of MIMIQ in a small-scale setup, focusing on the StateVector engine with between 10 to 20 qubits. Then, we’ll shift to MPS simulations, scaling from 10 to 100 qubits and testing various bond dimensions to observe its impact on performance and accuracy.
For these benchmarks, we used the following settings and environment:
- Quantum Simulators: MIMIQ-StateVector 0.16.1 and MIMIQ-MPS 0.15.1
- CPU: Intel(R) Xeon(R) E-2288G CPU @ 3.70GHz
- Circuit: Symmetry-preserving Ansatz in OpenQASM 2.0 format(all files used in this post were generated using the VeriQBench [6])
- MPS parameters: bond dimension = 64-512 (256– default parameters in MIMIQ)
- Qubit Range: StateVector: 10-20 (in steps of 2) MPS: 10-100 qubits (in steps of 10)
- Benchmark Metrics: Total RunTime and Fidelity of the final energy state
We use randomized VQE-like circuits, generated by VeriQBench script, where parameters for rotations are randomly chosen. The circuits apply a sequence of entangling gates and rotations across qubits, imitating the variational circuit structure commonly seen in VQE, but without targeting a specific Hamiltonian. Actual depth and complexity of the circuits are influenced by the number of qubits.
Results
The runtime and fidelity results of the MIMIQ benchmarks for VQE are illustrated in Figures 1, 2, and 3 below (note that Figures 1 and 2 use a logarithmic scale).
As shown in Figure 1, MIMIQ StateVector handles small circuits (10 – 20 qubits) very fast, but it becomes impractical around 22 qubits due to the exponential growth in computational requirements. For higher qubit numbers MIMIQ automatically switches to MPS for faster simulations. The MPS runtime also increases as the qubit count grows, but much slower, allowing us to simulate circuits of up to 100 qubits within minutes (Figure 2).
We characterize the accuracy of the MPS simulation using an estimate of the fidelity, which quantifies the overlap of the MPS with the exact solution. A fidelity of 1.0 means that the simulation is exact, whereas fidelity 0.5 means the MPS solution has at least 50% overlap with the exact solution. For example, using MIMIQ’s default bond dimension of 256, Figure 3 shows that the simulation is practically exact up to 40 qubits, and it begins to degrade beyond 60 qubits.
Importantly, fidelity can be improved by increasing the bond dimension. For example, at bond dimension 512, MPS can simulate up to 60 qubits close to exactly, and 80 qubits with at least 80% overlap with the exact solution. This increase in accuracy comes at the cost of increasing runtime (by about a factor of 5) as more memory is required to store the state. Conversely, one can speed up simulations at the cost of fidelity by reducing the bond dimension (see bd=64 and 128 data)––such approximate solutions can still capture the relevant aspects of some circuits, depending on the application (we will explore this in a future blogpost!).
The conclusion is that MPS can clearly go beyond state vector simulators using reasonable resources and can be tuned to find a balance between runtime and fidelity.
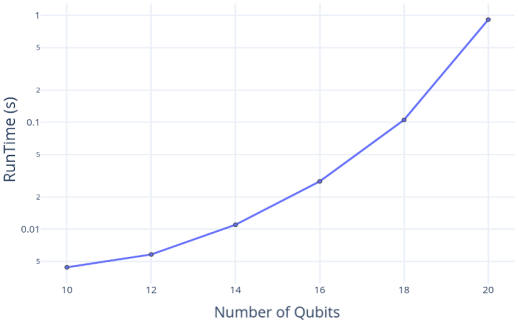
Fig. 1: Time to run a VQE circuit using MIMIQ StateVector as a function of qubit number.
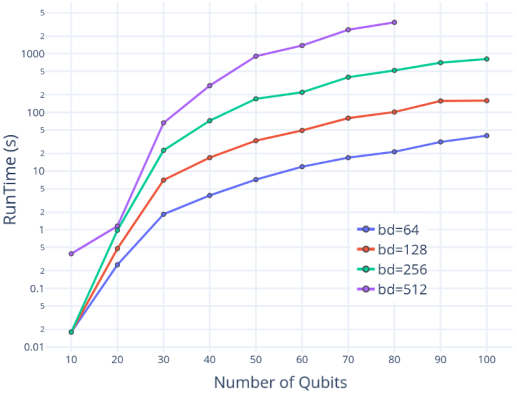
Fig. 2: Time to simulate a VQE circuit using MIMIQ MPS as a function of qubit number for different values of the bond dimension “bd”.
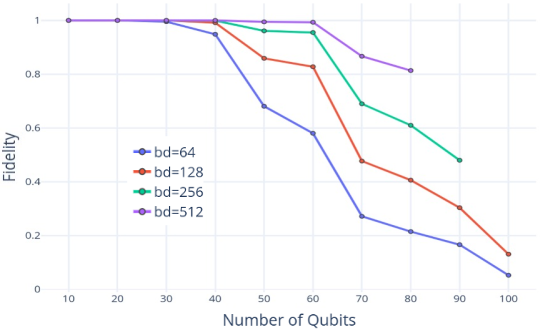
Fig. 3: Fidelity of simulating a VQE circuit using MIMIQ MPS as a function of qubit number for different values of the bond dimension “bd”.
Conclusion
MIMIQ’s dual-engine approach enables efficient scaling of VQE across varying numbers of qubits. For small circuits, the state vector engine provides exact and rapid solutions, while the MPS engine takes over beyond 20-30 qubits, allowing the simulation of significantly larger VQE quantum circuits. With MIMIQ, users can simulate small systems within milliseconds and tackle larger, complex systems—up to 100 qubits—in just minutes, while maintaining high fidelity. This capability opens the door to testing VQE solutions for real-world fields like chemistry and finance at large scales.
Finally, our results raise an important question: How does the quality of energy estimates, central to VQE, change with simulation fidelity? In a future blogpost we’ll examine the effects of fidelity degradation on VQE’s performance.
References:
[1] Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C., Endo, S., Fujii, K., … & Coles, P. J. (2021). Variational quantum algorithms. Nature Reviews Physics, 3(9), 625-644.
[2] Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y., … & Tennyson, J. (2022). The variational quantum eigensolver: a review of methods and best practices. Physics Reports, 986, 1-128.
[3] Peruzzo, A., McClean, J., Shadbolt, P., Yung, M. H., Zhou, X. Q., Love, P. J., … & O’brien, J. L. (2014). A variational eigenvalue solver on a photonic quantum processor. Nature communications, 5(1), 4213.
[4] Zhou, Y., Stoudenmire, E. M., & Waintal, X. (2020). What limits the simulation of quantum computers?. Physical Review X, 10(4), 041038.
[5] Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., & Gambetta, J. M. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature, 549(7671), 242-246.
[6] https://github.com/Veri-Q/Benchmark – VeriQBench is a benchmark for general tasks in Quantum Computing
If you too are interested in trying out MIMIQ, contact us!
https://qperfect.io/index.php/mimiq/ and reach out to us at contact@qperfect.io.
Read the MIMIQ press release


